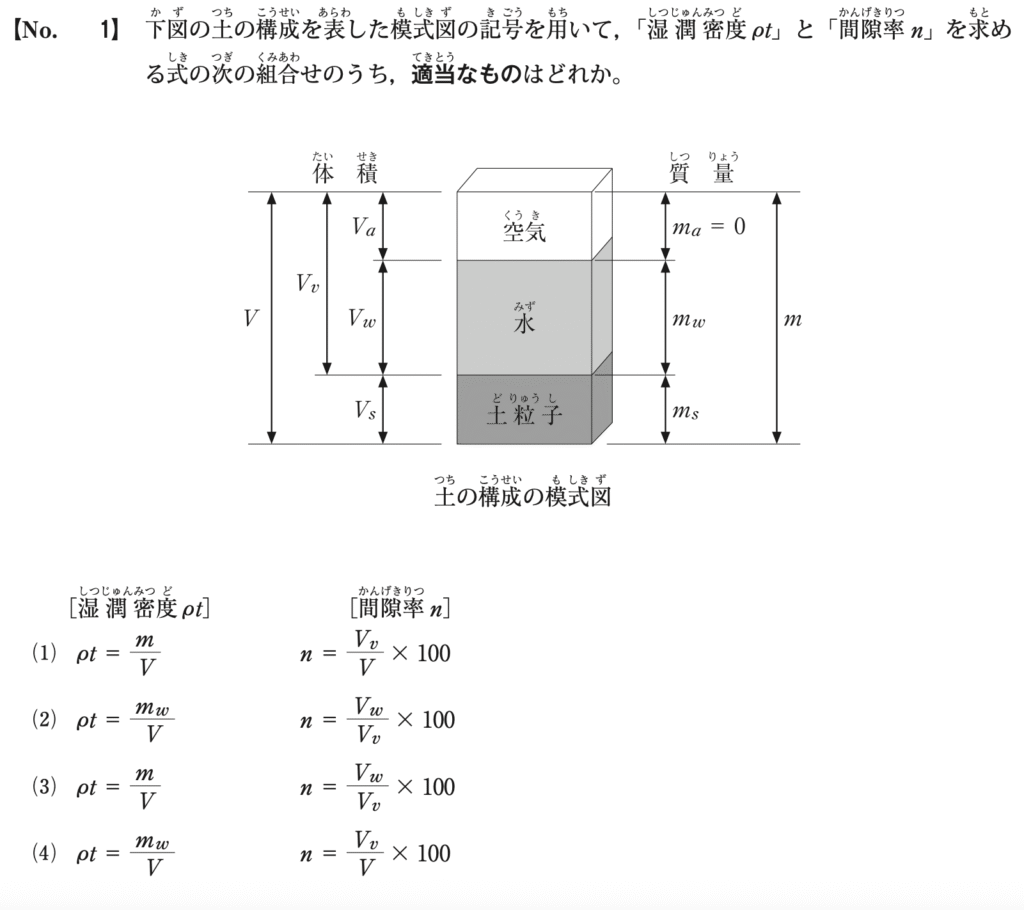
湿潤密度(pt) と間隙率(n) を求める適切な式の組み合わせは以下の通りです。
1.湿潤密度(pt)・・・土全体の質量(m)を土全体の体積(V)で割ったものです。したがってpt=m/Vとなります。
2.間隙率(n)・・・間隙の体積(Vv)を土全体の体積(V)で割ったもので、百分率で表します。したがって、n=Vv/V×100となります。
よって、これらの定義に合致するものは選択肢(1)である。 A=(1)
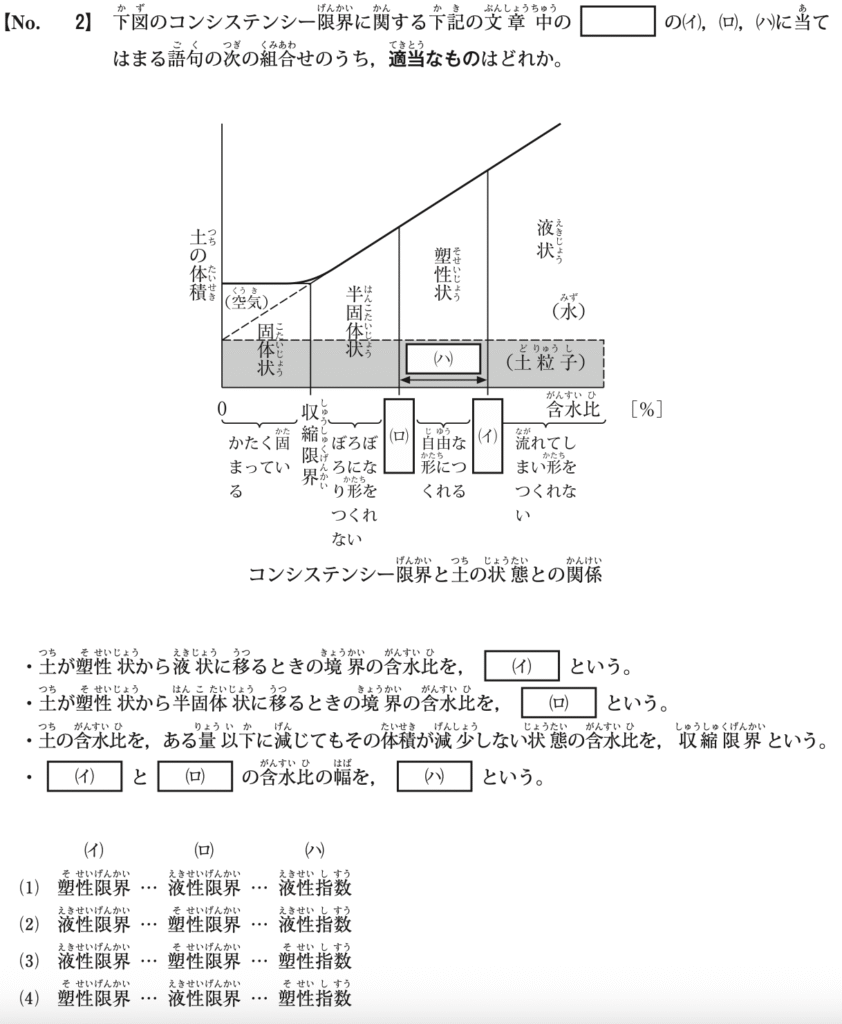
コンシステンシー限界に関する問題の解答は以下の通りです。
(イ)・・・土が塑性状から液体に移る時の境界の含水比は「液性限界」である。
(ロ)・・・土が塑性状から半個体状に移る時の境界の含水比は「塑性限界」です。
(ハ)・・・液性限界と塑性限界の含水比の幅は「蘇生指数」と呼びます。
したがって、適切な組み合わせは(3)です。 A=(3)
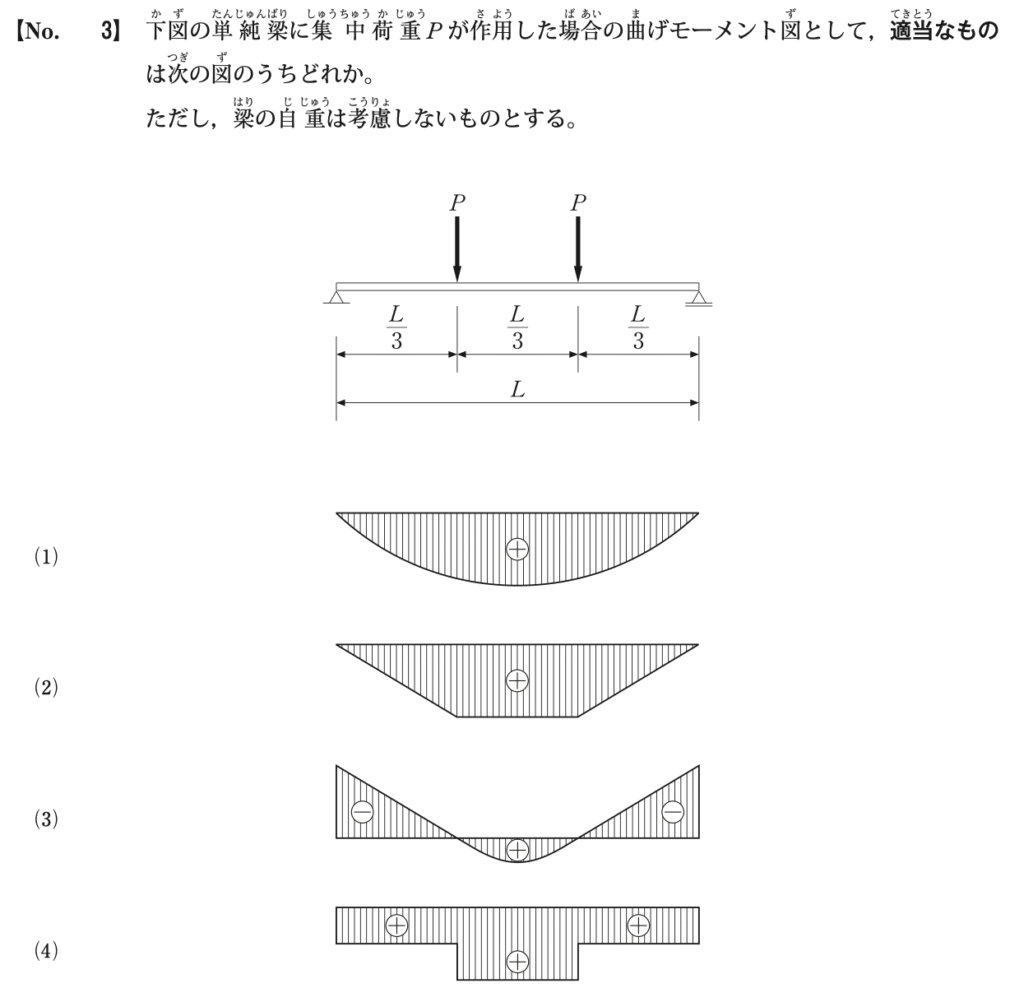
集中荷重下の単純梁の曲げモーメント・・・単純支持された梁に集中荷重が作用する場合、その点での曲げモーメントは最大となり、荷重点から支持点にかけては直線的に減少します。
今回のケース・・・図の梁は両端が単純支持されており、梁の中央から左右にL/3の位置にそれぞれ集中荷重Pが作用しています。この場合、それぞれの荷重点と支持点の間で曲げモーメントは直線的に変化します。
これらの特徴を総合すると、両側の荷重点から支持点にかけては直線的に減少し、中央の2つの荷重点の間では一定の曲げモーメントを示す図(2)が、この荷重条件における正しい曲げモーメント図となります。 A=(2)
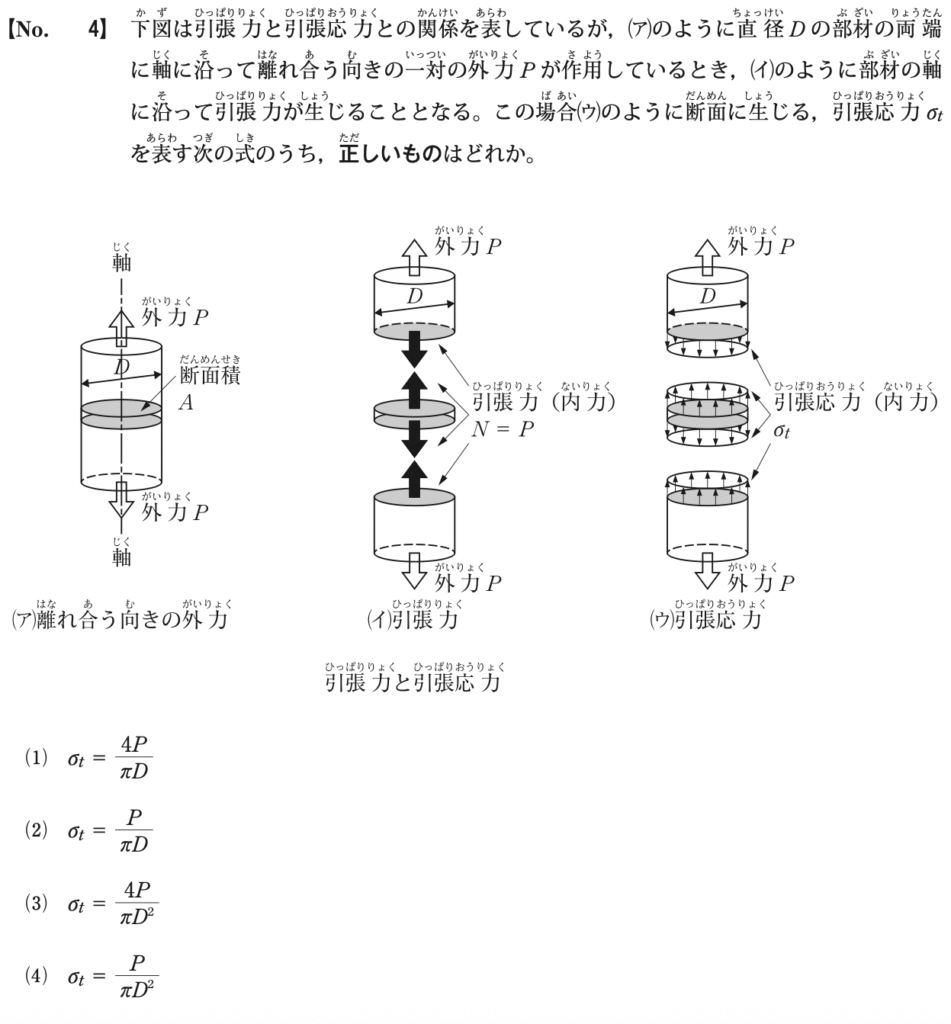
引張応力σtは、引張力Pを断面積Aで割ることで求められます。円形断面の断面積Aは、直径Dを用いて
A=π(D/2)^2=πD^2/4と表されます。
⒈引張応力の定義・・・引張応力σtは、引張力Pを断面積Aで割ったものである。σt=P/A
⒉断面積の計算・・・直径Dの円形断面の断面積Aは、以下の式で計算されます。
A=π(D/A)^2=πD^2/4
⒊引張応力σtの式への代入・・・上記の断面積Aの式を引張応力の定義式に代入すると、以下のようになります。
σt=P÷πD^2/4=4P/πD^2 となります。
したがって、正しい式は(3)σt=4P/πD^2 です。 A=(3)

この問題は、開水路におけるマニングの公式を用いて流量Qを求める問題です。
水深が管路の内径の半分であるため、半円形断面の開水路として扱います。
⒈潤辺Pと水路断面積Aの算出・・・水深がD/2の場合、水路の断面は半円形になります。
潤辺(水と接する部分の長さ)P=πD/2
水路断面積A=1/2×π(D/2)^2=πD^2/8
⒉径深Rの算出・・・径深R=A/P=πD^2/8÷πD/2=D/4
⒊マニングの公式の適用・・・マニングの公式は以下のようになります。
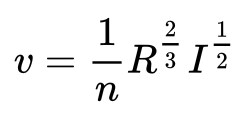
上記のAとRをを代入すると
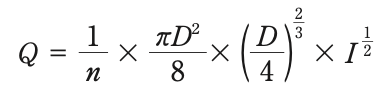
したがって、適当な式は(2)です。 A=(2)


コメント